集合的基本关系
(2)全集是研究问题的一个相对概念,研究的问题变了,全集有可能就变了,例如在整数集Z范围内研究问题时,全集就是整数集
要证明一个条件p是否是q的充要条件,需要从充分性和必要性两个方向进行,即证明两个命题“若p,则q”为真且“若q,则p”为真.
把集合中的元素逗号分隔一一列举出来,并用大括号“{}”括起来表示集合的方法叫作列举法.例如{-1,2,3,4}
在证明的过程中也可以转化为集合的思想来证明,证明p与q的解集是相同的,证明前必须分清楚充分性和必要性,即搞清楚由哪些条件推证到哪些结论.
小学集合数学知识点
例如:设p(x)中变量x的取值范围为集合M,则语句“对M的任一个元素x,有p(x)成立”是命题,叫作全称命题
)(2021-2022学年吉林*春市十一高中高一上学期中考试)下列命题中,既是存在量词命题又是真命题的是()
例1.(2020-2021学年*省梅州市梅江区梅州中学高一上学期第一次段考)“三角形的某两条边相等”是“三角形为等边三角形”的()
把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解.
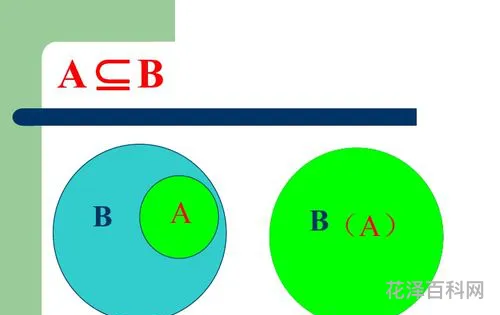
集合之间存在几种关系
补集的定义:对于全集的一个子集A,由全集中不属于A的所有元素组成的集合,称为集合A相对于全集的补集,简称为集合A的补集
此题的难点在于将两集合中的代表元素形式化为相似结构,因此对于集合中表达式是分式型的,可通过通分,化为同分母,消除结构上的差异,再找出两集合之间的关系.
差集运算是指从一个集合中去掉与另一个集合共有的元素后所剩下的部分,记作A-B。即A-B={x|x∈A且x∉B}。
在解决数学问题时,我们经常需要找出满足多个条件的元素的集合,这时就可以利用并集运算。例如,求解不等式组的解集时,可以通过并集运算将各个不等式的解集合并起来。








添加新评论