角加速度公式_专栏

设在时刻t和t┡刚体的角速度矢量分别是ω和ω',令Δω=ω'ω,则Δω表示刚体的角速度在时间间隔Δt=t't内的改变量。比值称为刚体在时间Δt内的平均角加速度,而极限表示在瞬时t刚体角速度ω的真实变化情况,σ称为刚体的角加速度矢量。

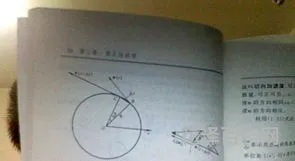
角加速度公式

当刚体作定点运动时,角加速度矢量σ表示瞬时角速度矢量ω对时间的变化率,但和刚体作定轴转动不同,ω和σ是不共线的,ω的方向沿瞬时转动轴,而σ的方向则可由矢量ω的端点A的线速度v来表示(图2)。角加速度的量纲是T-2,它的SI单位是rad/s2。

保守力:做功只与物体起点和终点的位置有关,与物体所通过的路径无关的力叫做保守力,例如重力、万有引力、弹力、静电力等。

这篇文章主要罗列大学物理里面的力学知识点与公式,主要包括质点运动学,质点动力学、刚体力学以及能量问题,没有涉及流体力学和振动波动的内容。

)采用牛顿的绝对时空观念认为时间和空间彼此*,时间间隔和空间间隔的测量与参考系选择无关,这样前提下的变换称为伽利略变换,其主要关系为:

非保守力:做功不但与物体起点、终点的位置有关还与物体所通过的路径有关的力叫做非保守力,例如磁力、摩擦力等。

举例:假如两辆汽车开始静止,均匀地加速后,达到10m/s的速度,a车花了10s,而b车只用了5s。它们的速度都从0m/s变为10m/s,速度改变了10m/s。所以它们的速度变化量是一样的。但是很明显,b车变化得更快一些。我们用加速度来描述这个现象:b车的加速度(a=v/t,其中的v是速度变化量)

加速度为零时,物体静止或做匀速直线运动(相对于同一参考系)。任何复杂的运动都可以看作是无数的匀速直线运动和匀加速运动的合成。

定义:连接运动质点和圆心的半径在单位时间内转过的弧度叫做角速度。它是描述物体转动或一质点绕另一质点转动的快慢和转动方向的物理量。

显然,当速度变化量一样的时候,花时间较少的b车,加速度更大。也就是说b车的启动*能相对a车好一些。因此,加速度是表示速度变化的快慢的物理量。

在匀变速直线运动中,平均速度还可以用(v0+vt)2来计出,此时平均速度还表示通过这段位移所用的时间的中间时刻的瞬时速度。

匀速圆周运动中的角速度:对于匀速圆周运动,角速度是一个恒量,可用运动物体与圆心联线所转过的角位移和所对应的时间t之比表示=△/△t,还可以通过v(线速度)/r(半径)求出。

角加速度公式