梯形面积公式_热门

通过观察图形可知,第一块钢板的面积是梯形和三角形的面积之和,第二块钢板的面积是长方形的面积减去梯形的面积。通过读图,找出相关的隐藏条件,再运用公式进行计算。

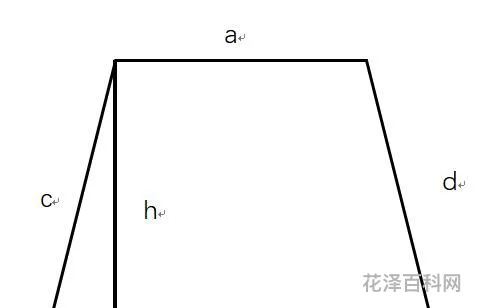
重点是根据图形的特点确定这个直角梯形的上底和下底的长度。由题意可知:左右两个三角形都是等腰直角三角形,所以

梯形面积公式

有一批圆木堆成梯形,最上面一层有3根,最下面一层有8根,相邻两层相差1根,一共堆了6层,这堆圆木共有()根。

先依据平行四边形的面积公式计算出整个图形的面积,将该面积加上18平方厘米再除以2就是梯形的面积,最后利用梯形的面积公式计算出上底的长。

根据平行四边形的特点,底边上的高一定小于另一条底边,所以高为5厘米对应的底为4厘米,再根据面积公式计算。在分析时,可让学生通过画图的方式得出类似结论并加以强化。

根据“(顶层根数+底层根数)×层数÷2”进行解答。在此基础上,可引导学生用不同的方法对结果加以验证,重点分析采用等差数列求和的方法即“(首项+末项)×项数÷2”,这既是解决该题的基本数学模型,也能突出体现“数形结合”的思想。

引导学生仔细观察图形,得出涂色部分三角形与整个平行四边形存在等底等高的关系,则该三角形的面积应为平行四边形面积的一半,据此进一步推导出涂色三角形的面积和两个空白三角形的面积之和相等这一结论。

若要转载原创文章用于商业用途,请联系我们,未经同意不得转载。任何转载请注明文章来源。如有问题,请联系我们,谢谢!

直接利用公式计算这三种图形的面积,对于学生来说完成的难度不大。对于已知平行四边形的面积和高求底、已知三角形的面积和底求高这两个变式练习,可引导学生进行比较,理解并强化三角形和梯形的类似计算中需要先将“面积×2”这一知识点。

下图是一个平行四边形,它包含了三个三角形,其中两个空白三角形的面积分别是15平方厘米和25平方厘米。中间涂色三角形的面积是()。

三角形的面积=底×高÷2,而图中甲、乙、丙3个三角形等底等高,所以面积都相等。也可以引导学生探索3个三角形与各自所在正方形的面积关系,发现每个三角形的面积都等于正方形面积的一半。

通过转化,小花瓶左右两侧的部分可以组合成两个小正方形,再加瓶身的部分即可。也可采用计算的方法,由题意可得一个小正方形的边长为1厘米,则花瓶两边三角形的面积之和为2×1÷2×2=2(平方厘米),整个花瓶的面积为2+3=5(平方厘米)。

因为等底等高的平行四边形面积是三角形面积的2倍,由图形可知,平行四边形和三角形的高相等,要使平行四边形的面积是三角形的3倍,只要平行四边形的底是三角形底的1.5倍即可;在高相等的情况下,要使梯形的面积和平行四边形的面积相等,只要梯形的上下底之和的一半等于平行四边形的底即可。

梯形面积公式